
This is because the relative position of objects changes as the observer's perspective changes, or is differently viewed with each eye. Thus, no obvious reversal of any sort can be seen in the mirror image of the urn.Ī mirror image appears more obviously three-dimensional if the observer moves, or if the image is viewed using binocular vision. In the example of the urn and mirror (photograph to right), the urn is fairly symmetrical front-back (and left-right). Notice that there is no obvious front-back or left-right of the mountain. In the picture of the mountain reflected in the lake (photograph top right), the reversal normal to the reflecting surface is obvious. Therefore, no matter how the object is oriented towards the mirror, all the resulting images are fundamentally identical (as Corballis explains in his paper "Much ado about mirrors", mentioned above). However, it's important to understand that there are always only two enantiomorphs, the object and its inside-out image. If a person stands side-on to a mirror, left and right hands will be reversed directly by the mirror, because the person's left-right axis is then normal to the mirror plane. If one looks in a mirror two axes (up-down and left-right) coincide with those in the mirror, but the third axis (front-back) is reversed. Reflection in a mirror does result in a change in chirality, more specifically from a right-handed to a left-handed coordinate system (or vice versa). The psychology of the perceived left-right reversal is discussed in "Much ado about mirrors" by Professor Michael Corballis (see "external links", below). The perception of a left-right reversal is geometrically explained by the fact that a three-dimensional object seen in a mirror is an inside-out version of the actual object, like a glove stripped off the left hand and turned into a right-hand glove, but there is still some confusion about the explanation amongst psychologists. Hence, the reversal is somewhat misleadingly called a "lateral inversion". Although a plane mirror reverses an object only in the direction normal to the mirror surface, this turns the entire three-dimensional image seen in the mirror inside-out, so there is a perception of a left-right reversal. Thus reflection is a reversal of the coordinate axis perpendicular ( normal) to the mirror's surface. If a point of an object has coordinates ( x, y, z) then the image of this point (as reflected by a mirror in the y, z plane) has coordinates (− x, y, z). In general, an object and its mirror image are called enantiomorphs. That is an example of chirality (chemistry). In chemistry, two versions (isomers) of a molecule, one a "mirror image" of the other, are called enantiomers if they are not "superposable" (the correct technical term, though the term "superimposable" is also used) on each other. More fundamentally in geometry and mathematics they form the principal objects of Coxeter group theory and reflection groups. In physics, mirror images are investigated in the subject called geometrical optics. A three-dimensional object is reversed in the direction perpendicular to the mirror surface.
The term then relates to structural as well as visual aspects. The concept of reflection can be extended to three-dimensional objects, including the inside parts, even if they are not transparent. In three dimensions A symmetrical urn and its mirror image So, in these examples the mirror does not actually cause the observed reversals. Again we perceive a left-right reversal due to a change in our orientation. Then we compare the object with its reflection by turning ourselves 180°, towards the mirror. Another example is when we stand with our backs to the mirror and face an object that is in front of the mirror.
In this example, it is the change in orientation rather than the mirror itself that causes the observed reversal. If we first look at an object that is effectively two-dimensional (such as the writing on a card) and then turn the card to face a mirror, the object turns through an angle of 180° and we see a left-right reversal in the mirror.

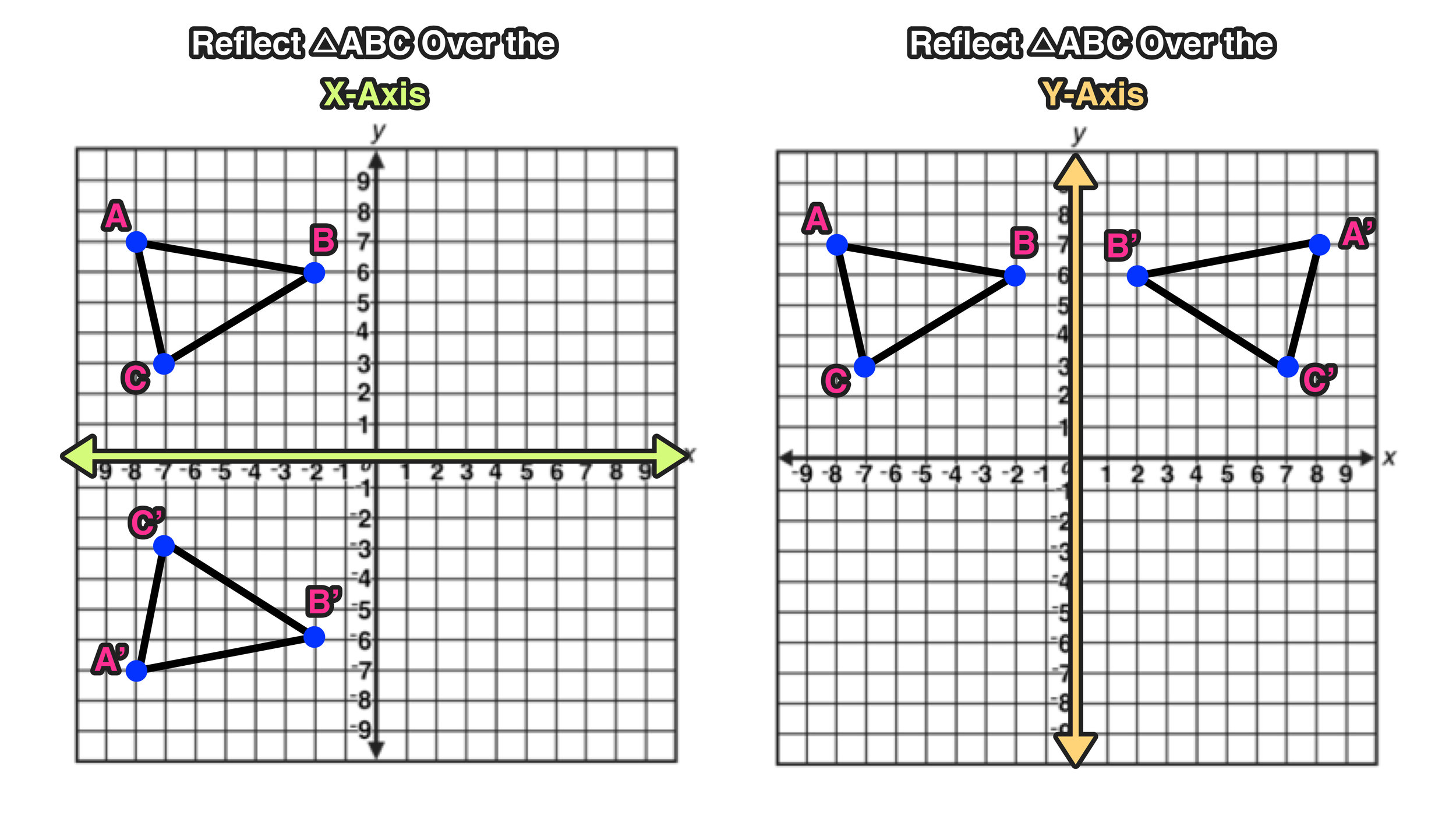
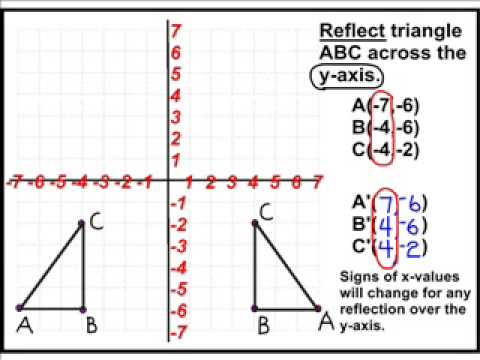
Two-dimensional mirror images can be seen in the reflections of mirrors or other reflecting surfaces, or on a printed surface seen inside-out. In geometry, the mirror image of an object or two-dimensional figure is the virtual image formed by reflection in a plane mirror it is of the same size as the original object, yet different, unless the object or figure has reflection symmetry (also known as a P-symmetry).


 0 kommentar(er)
0 kommentar(er)
